Continuous Random Variable Example

By Ra_Xiomara703 02 Sep, 2022 Post a Comment

Consider an example of tossing of two fair coins. Note that before differentiating the CDF we should check that the CDF is continuous.

Continuous Random Variable Definition Examples Explanation

The discrete random variable X on rolling dice can take on values from 1 to 6.

. It may be any set. As we will see later the function of a continuous random variable might be a non-continuous random variable. The importance of the normal distribution stems from the Central Limit Theorem which implies that many random variables have normal distributionsA little more accurately the Central Limit Theorem says.

If in the study of the ecology of a lake X the rv. A continuous random variable Y and a binary random variable X which takes the values zero and one. X is a continuous random variable with probability density function given by fx cx for 0 x 1 where c is a constant.

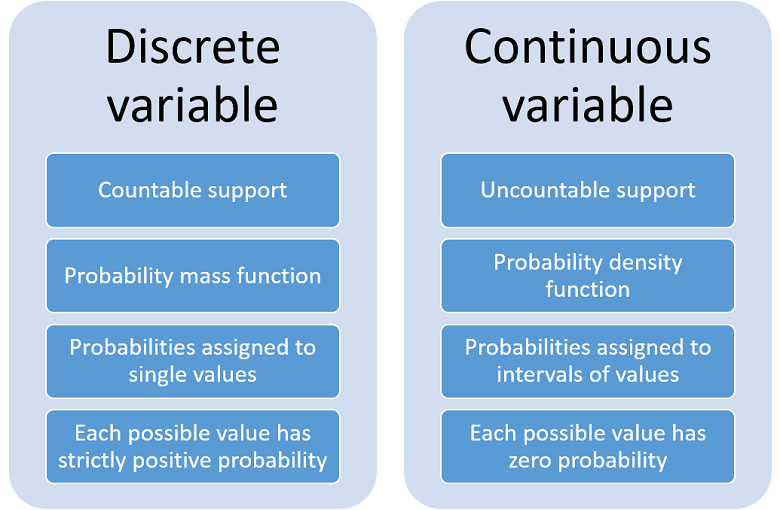
Implicit in the definition of a pmf is the assumption that it. If X is a discrete random variable with discrete values x. There are no gaps in between which would compare to numbers which have a limited probability of occurring.

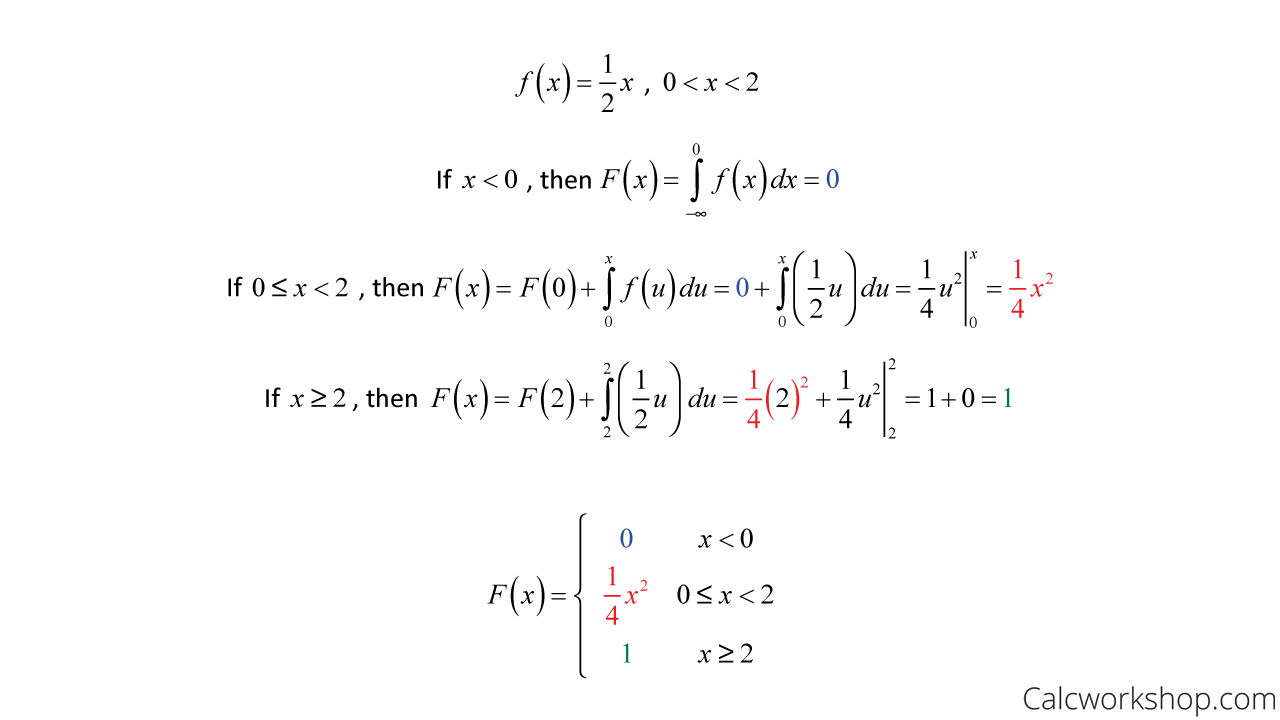
CDFs are also defined for continuous random variables see Chapter 4 in exactly the same way. Then X is a continuous rv. The uniform distribution is the simplest continuous random variable you can imagine.

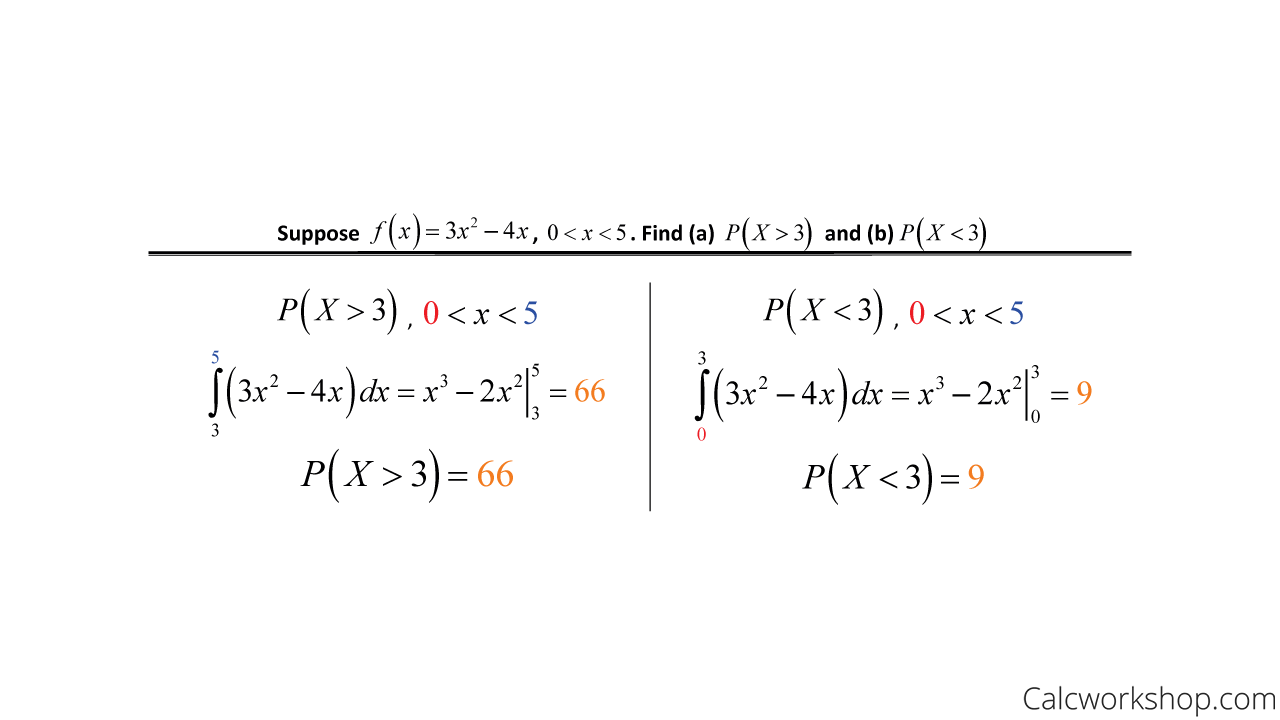
A Cauchy random variable takes a value in with the fol-lowing symmetric and bell-shaped density function. The range for X is the minimum. If we integrate fx between 0 and 1 we get c2.

Suppose that we want to simulate a random variable X that follows the exponential distribution with mean λ ie. Second the cdf of a random variable is defined for all real numbers unlike the pmf of a discrete random variable which we only define for the possible values of the random variable. So if a variable can take an infinite and uncountable set of values then the variable is referred as a continuous variable.

Fx 1 π1xµ2. The probability density function or PDF of a continuous random variable gives the relative likelihood of any outcome in a continuum occurring. Continuous-variable CV quantum information is the area of quantum information science that makes use of physical observables like the strength of an electromagnetic field whose numerical values belong to continuous intervals.

Find the mean value for the continuous random variable fx x 0 x 2. It is often referred to as the bell curve because its shape resembles a bell. Probability Distribution of a Continuous Random Variable.

Continuous variable as the name suggest is a random variable that assumes all the possible values in a continuum. Probability density functions Opens a modal. Lets look at an example.

The expectation of Bernoulli random variable implies that since an indicator function of a random variable is a Bernoulli random variable its expectation equals the probability. It is usually more straightforward to start from the CDF and then to find the PDF by taking the derivative of the CDF. Fig42 - PDF for a continuous random variable uniformly distributed over ab.

The variance of the random variable is 074 Thats it. One primary application is quantum computingIn a sense continuous-variable quantum computation is analog while quantum computation using. Examples of distributions with continuous random variable are exponential random variable and normal random variable.

First we implement this method for generating continuous random variables. A random variable X is continuous if possible values comprise either a single interval on the number line or a union of disjoint intervals. What is the mean of a discrete random variable on rolling a dice.

Unlike the case of discrete random variables for a continuous random variable any single outcome has probability zero of occurring. Simply put it can take any value within the given range. Probability with discrete random variable example Opens a modal Mean expected value of a discrete random variable.

The probability of occurrence of each value is 1 6. The PDF fx satisfies the following two properties. Difference between random variable and random process For example we can collect the random signal temperature Tt.

If the common product-moment correlation r is calculated from these data the resulting correlation is called the point-biserial correlation. Khan Academy is a 501c3 nonprofit organization. Hence we have four different types of random process.

We know that the Probability Distribution Function PDF of the exponential distribution is. Yes the question in the OP - particularly the summary - was poorly phrased. Mean and standard deviation of a binomial random variable Get 3 of 4 questions to level up.

Perhaps if we had focused on the CDF it would have been less of a surprise that the CDF of the discrete variable is equal to the CDF of the normal distribution at each integer step and therefore less of a surprise that the CDF is 1 at. Definition of Continuous Variable. Formally a continuous random variable is such whose cumulative distribution function is constant throughout.

The possible outcomes for this random experiment are S HH HT TH TT. Random processes can be discrete or continuous - meaning the outcome variable has a discrete or continuous range - and can occur in discrete or continuous time. This is a useful fact.

Assume that n paired observations Yk Xk k 1 2 n are available. If X is a random variable for the occurrence of the tail the possible values for X are 0 1 and 2. May be depth measurements at randomly chosen locations.

A set of real numbers a set of vectors a set of arbitrary non-numerical values etcFor example the sample space of a coin flip would be. For any continuous random variable with probability density function fx we have that. For other types of continuous random variables the PDF is non-uniform.

Variance of a Discrete Random Variable Probability Table Question. We should not be talking about a PDF of a discrete variable. Constructing a probability distribution for random variable Our mission is to provide a free world-class education to anyone anywhere.

44 Normal random variables. PDF for a continuous random variable can be described by the integral 1. The probability density function gives the probability that any value in a continuous set of values.

The normal distribution is the most important in statistics. A probability distribution is a mathematical description of the probabilities of events subsets of the sample spaceThe sample space often denoted by is the set of all possible outcomes of a random phenomenon being observed.

Continuous Random Variables Example 1 Youtube